Let C denote the set of complex numbers, and suppose U is some subset of C. As such, their properties are easily deduced from properties of the exponential function.Ĭomplex-valued functions defined on a subset of complex numbers may (some times) be differentiated, yes. The hyperbolic functions are usually defined in terms of the exponential function.
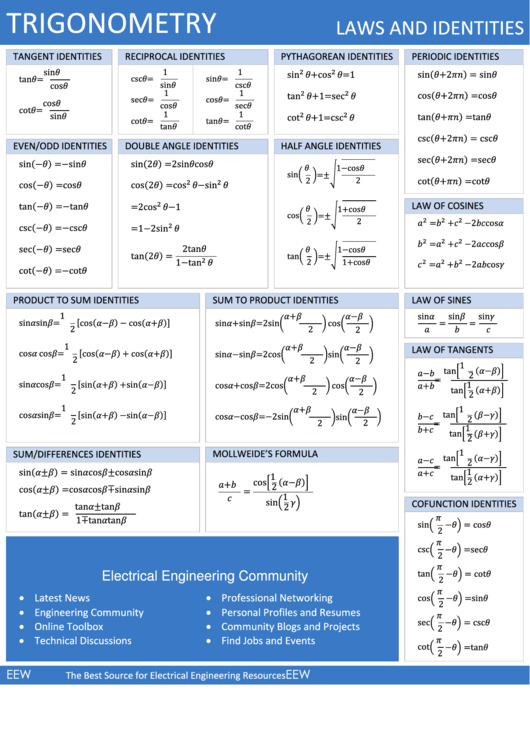
It is important to know the inverse trig functions as they come in handy in many situations, like trig substitution in integral calculus.
Or, using the term arcsin and not sin^-1 (though sin^-1 is more common) Like the square/square root example, if you have y=sin(x), which is y in terms of x, but you want to take that expression and find x in terms of y, then given: It is the same deal with sin and arcsin, which is conventionally written as sin^-1 x.Īrcsin is the inverse of sin, such that arcsin(sin(x)) = x, or sin(arcsin(x))=x. Now if you want to find out what x is in terms of y, then solve for x to get x=√y.Īs you know, the square operator and the square root operator are inverses of each other, that is, one 'undoes' the other: √(x²) = (√x)² = x (assuming we are only interested in the principal square root).